由于LTI系统满足齐次性、可加性和时不变性,因此如果能把任意输入信号分解成基本信号的线性组合,那么只要得到了LTI系统对基本信号的响应,就可以利用系统的线性特性,将系统对任意输入信号产生的响应表示成系统对基本信号的响应的线性组合。作为基本信号,应当满足下面两个条件:
-
本身应尽可能简单,并且用它的线性组合能够表示尽可能广泛的其他信号;
-
LTI系统对这种信号的响应易于求得。
离散时间LTI系统:卷积和(Convolution Sum)
用单位脉冲表示离散时间信号
离散时间信号中,最简单的是$ \delta[n] $,可以由它的线性组合构成$ u[n] $,即:
对任意的离散时间信号$ x[n] $,如果每次从其中取出一个点,就可以将信号拆开,每次取出的点都可以表示为不同加权、不同位置的单位脉冲。
因此有:$ x[n] = \sum_{k=-\infty}^{\infty}{x[n]\delta[n-k]} $
这个式子表明:任何的信号$ x[n] $都可以被分解成移位加权的单位脉冲信号的线性组合。
卷积和
如果一个线性系统对$ \delta[n-k] $ 的响应是$ h_k[n] $,则由线性特性就有对任何输入$ x[n] $的响应为:
如果系统具有时不变性:若$ \delta[n] \rightarrow h[n] $, 则$ \delta[n-k] \rightarrow h[n-k] $
因此只要得到了LTI系统对$ \delta[n] $ 的响应$ h[n] $,就可以得到LTI系统对任何输入信号$ x[n] $的响应:
其中:$ h[n] $称为单位脉冲响应(Impulse Response)
这表明:一个LTI系统可以完全由它的单位脉冲响应来表征。这种求得系统响应的运算关系称为卷积和(Convolution Sum)。
卷积和的计算
将一个信号$ x[k] $不动,另一个信号经过反转后称为$ h[-k] $,再将参变量$ n $移位。在每个n值的情况下,将$ x[k] $和$ h[-k] $对应点相乘,再把乘n积的各点值累加,即得到$ n $时刻的$ y[n] $。
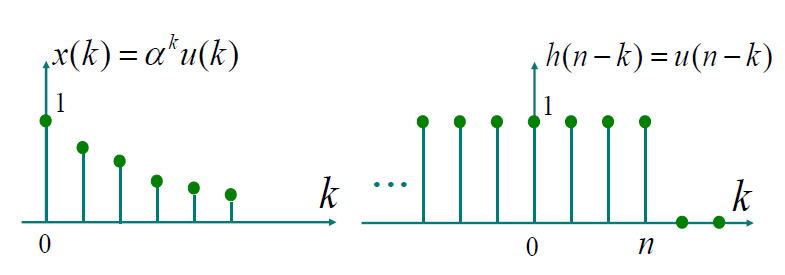
E.g. 求卷积和:$ x[n]=\alpha ^nu[n]\qquad 0<\alpha<1 \qquad h[n]=u[n] $(点击问题查看答案)
E.g. 求卷积和:$ x[n] = \begin{cases} 1 & 0\leq n\leq 1 \\ 0 & \text{ otherwise } \end{cases} \qquad h[n] = \begin{cases} \alpha^n & \alpha>1, 0 \leq n \leq 6 \\ 0 & \text{ otherwise } \end{cases} $(点击问题查看答案)
连续时间LTI系统:卷积积分(Convolution Integral)
用冲激信号表示连续时间信号
与离散时间信号分解的思想相一致,连续时间信号应该可以分解成一系列移位加权的单位冲激信号的线性组合。至少单位阶跃与单位冲激之间有这种关系:
而对于一般信号$ x(t) $,可以将其分成很多$ \Delta $宽度的区段,用一个阶梯信号$ x_\Delta(t) $近似表示$ x(t) $。当$ \Delta \rightarrow 0 $时,有$ x_\Delta(t) \rightarrow x(t) $
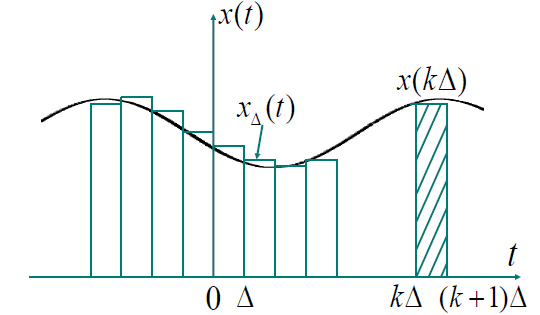
引用$ \delta_\Delta (t) $,即:
, 则有:
第$ k $个矩形可表示为:$ x(k\Delta)\delta_\Delta(t-k\Delta)\cdot \Delta $,这些矩形叠加起来就成为阶梯形信号$ x_\Delta(t) $,即:
当$ \Delta \rightarrow 0 $时,$ k\Delta \rightarrow \tau \qquad \Delta \rightarrow d\tau \qquad \sum \rightarrow \int \qquad \delta_\Delta(t-k\Delta) \rightarrow \delta(t-\tau) \qquad x_\Delta(t) \rightarrow x(t) $
这表明:任何连续时间信号$ x(t) $都可以被分解成移位加权的单位冲激信号的线性组合。
卷积积分(Convolution Integral)
与离散时间系统的分析类似,如果一个线性系统对$ \delta(t-\tau) $的响应为$ h_\tau(t) $,则该系统对$ x(t) $的响应可以表示为:$ y(t) = \int_{-\infty}^{\infty}{x(\tau)h_\tau(t)d\tau} $
若系统是时不变的,即若$ \delta(t) \rightarrow h(t) $,则 $\delta(t-\tau) \rightarrow h(t-\tau) $,于是系统对任意输入$ x(t) $的响应可表示为: $ y(t) = \int_{-\infty}^{\infty}{x(\tau)h(t-\tau)d\tau} = x(t) \ast h(t) $
这表明:LTI系统可以完全由它的单位冲激响应$ h(t) $来表征。这种求得系统响应的运算关系称为卷积积分(Convolution Integral)。
卷积积分的计算
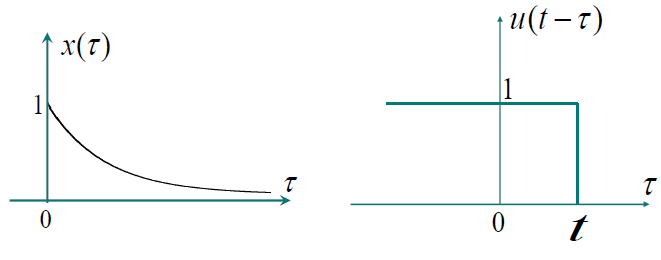
卷积积分的计算与卷积和类似:参与卷积的两个信号中,一个不动,另一个反转后随参变量$ t $移动。对每一个$ t $的值,将$ x(\tau) $和$ h(t-\tau) $对应相乘,再计算相乘后曲线所包围的面积。通过图形帮助确定积分区间和积分上下限是很有用的。
E.g. 求卷积积分:$ x(t) = e^{-at}u(t), \quad a > 0 \quad h(t) = u(t) $(点击问题查看答案)
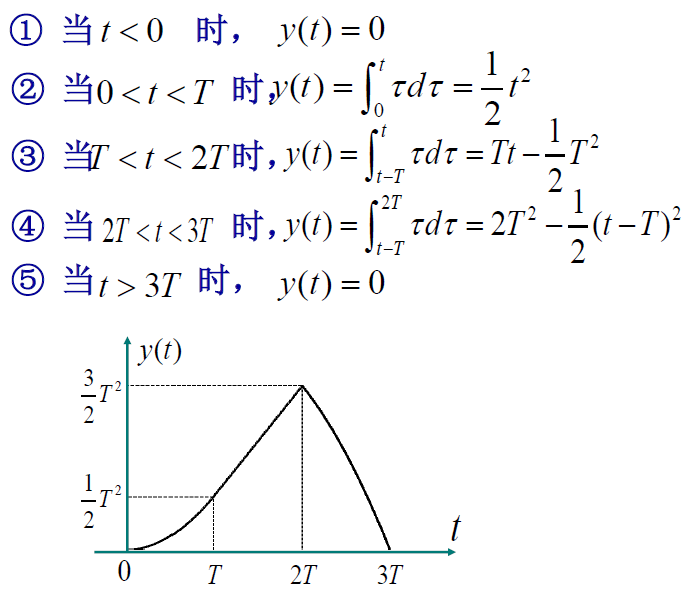
E.g. 求卷积积分:$ x(t) = \begin{cases} 1 & 0 < t < T \\ 0 & \text{ otherwise } \end{cases} \qquad h(t) = \begin{cases} t & 0 < t < 2T \\ 0 & \text{ otherwise } \end{cases} $(点击问题查看答案)
线性时不变系统的性质
卷积积分和卷积和的性质
1. 交换律
2. 分配律
3. 结合律
4. 微积分/求和求差与时移特性
-
卷积积分满足微分、积分及时移特性($ x(t) \ast h(t) = y(t) $)
①$ \begin{align*} &{x}'(t) \ast h(t) = x(t) \ast {h}'(t) = {y}'(t) \\&[\int_{-\infty}^{t}x(\tau)d\tau] \ast h(t) = x(t) \ast [\int_{-\infty}^{t}h(\tau)d\tau] = \int_{-\infty}^{t}y(\tau)d\tau \end{align*} $②$ x(t-t_0) \ast h(t) = x(t) \ast h(t-t_0) = y(t-t_0) $ -
卷积和满足差分、求和及时移特性($ x[n] \ast h[n] = y[n] $)
①$ \begin{align*} &(x[n]-x[n-1]) \ast h[n] = x[n] \ast {h}'[n] = y[n]-y[n-1] \\ &[\sum_{k=-\infty}^{n}x[k]] \ast h[n] = x[n] \ast [\sum_{k=-\infty}^{n}h[k]] = \sum_{k=-\infty}^{n}y[k] \end{align*} $②$ x[n-n_0] \ast h[n] = x[n] \ast h[n-n_0] = y[n-n_0] $
恰当地利用卷积的性质可以简化卷积的计算:
E.g. 求卷积积分:$ x(t) = \begin{cases} 1 & 0 < t < T \\ 0 & \text{ otherwise } \end{cases} \qquad h(t) = \begin{cases} t & 0 < t < 2T \\ 0 & \text{ otherwise } \end{cases} $(点击问题查看答案)
LTI系统的性质
1. 记忆性
2. 可逆性
3. 因果性
4. 稳定性
用微分/差分方程描述的因果LTI系统
这里不做过多数学上的要求,但是对于离散时间系统需要清楚FIR (finite inpulse response)系统与IIR (finite inpulse response)系统的区别:当系统的差分方程为递归方程时,系统为IIR系统,反之则为FIR系统;或者通过系统某一时刻的输出是否与之前的输出有关,若与之前的输出有关,则系统为IIR系统,反之为FIR系统。
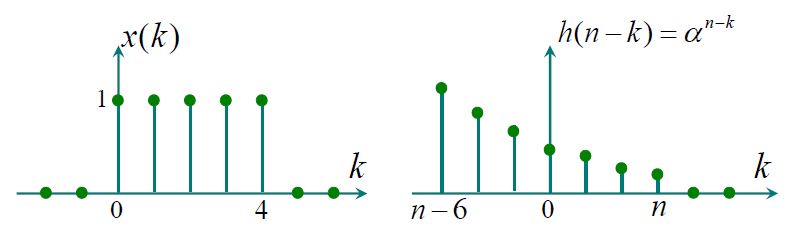
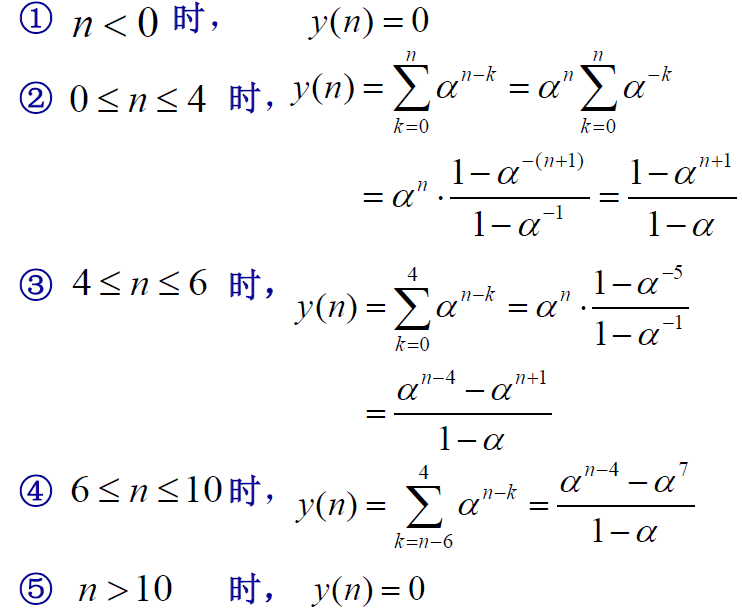
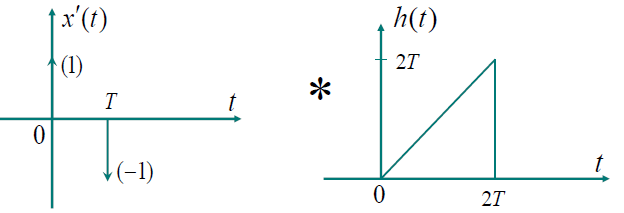 根据微分特性有:
$ \begin{align*} y'(t) &= x'(t) \ast h(t) = h(t) \ast [\delta(t) - \delta(t-T)] \\ &=h(t) - h(t - T) \end{align*} $
根据微分特性有:
$ \begin{align*} y'(t) &= x'(t) \ast h(t) = h(t) \ast [\delta(t) - \delta(t-T)] \\ &=h(t) - h(t - T) \end{align*} $
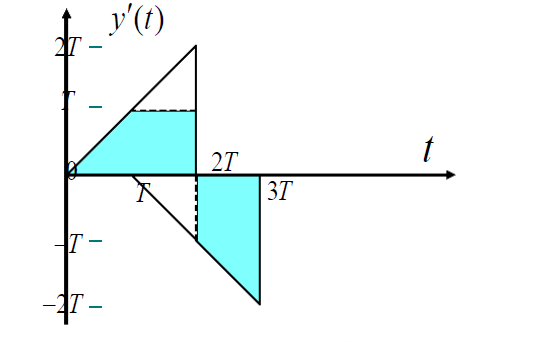 再利用积分特性:
再利用积分特性: