试题共七道大题,小题并不能回忆起全部内容,还请见谅;其中选择题记不清选项,可以作为填空题练习。
试题仅仅由考试后回忆记录,并无任何作弊行为,仅供后续学弟学妹提供复习参考;文字并不是试卷的完整的表述,仅代表个人对题意的理解。
点击题目可查看个人计算结果,仅供参考,如有错误请联系我。
一、判断题(共六题)
- 离散时间信号与其在扩展域上的零极点图是一一对应的
- 有限的点长信号通过点长有限的系统的输出信号点长大于等于输入信号的点长
- 单位脉冲函数是离散时间LTI系统的特征函数
二、单选题(共六题)
- $ \sin [\frac{15\pi }{32}n] $ 的基波周期
- 一离散时间系统有一个极点为 $ \frac{8}{9} $ ,有一个零点为0,这个系统是什么系统(低通/高通/带通/带阻)
- 已知 $ h[n] $ 为一个低通系统,则$ (-1)^n h[n] $是什么系统(低通/高通/带通/全通)
- $ h(t) $稳定的充要条件
三、计算题
1. 已知$ x[n]= u[n+1] - u[n-2] $,$ h[n] = (n+1) u[n] - u[n-3] $ ,求$ y[n] $,并画出$ y[n] $
2. 已知$ x(t) $的傅里叶变换为$ X(j\omega) $,$ y(t) = x(2t-1) + x(t/3) $,试用$ X(j\omega) $表示$ Y(j\omega) $
3. 已知$ x(t) = \sum_{k=0}^{3}(\frac{1}{2}) ^{k}\cos (3k\pi) $,现通过一个单位脉冲响应$ h(t) = \frac{\sin4t}{\pi t} $的系统,求$ y(t) $
4. 将$ X(z) $的z反变换$ x[n] $表示成下述的形式: $$ x[n] = x[0]\delta[n] + x[1]\delta[n-1] + --- +x[4]\delta[n-4] \\ X(z) = \frac{2+z^-1}{2+3z^{-1}+z^{-2}} $$
四、 已知$ x[n] = \delta[n+1] + \delta[n] +\delta[n-1] $
1. 求$ X(j\omega) $
2. 求$ \int_{-\pi}^{\pi}\left | X(j\omega) \right |^2 d\omega $ 和 $ \int_{-\pi}^{\pi} X(j\omega) d\omega $
3. 将x[n]进行周期延拓作为$ \tilde{x}[n] $,设$ N = 5 $,试求$ \tilde{x}[n] $的傅里叶级数的系数 $ a_k $
五、 根据系统的零极点图求解以下问题:
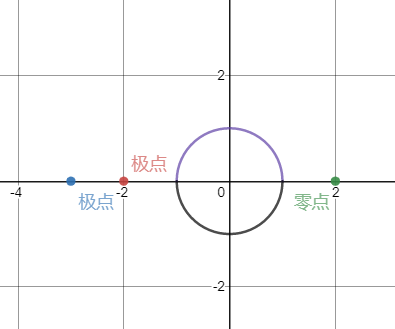
1. 求$ H(s) $,已知$ H(0) = -1 $
2. 求系统的微分方程与$ h(t) $
3. 当$ x(t) = e^-tu(t) $ 时,求$ y(t) $
4. 当$ x(t) = \cos 3t $时,求输出的幅值改变大小
六、 已知该系统的初始状态是松弛的,求解以下问题:
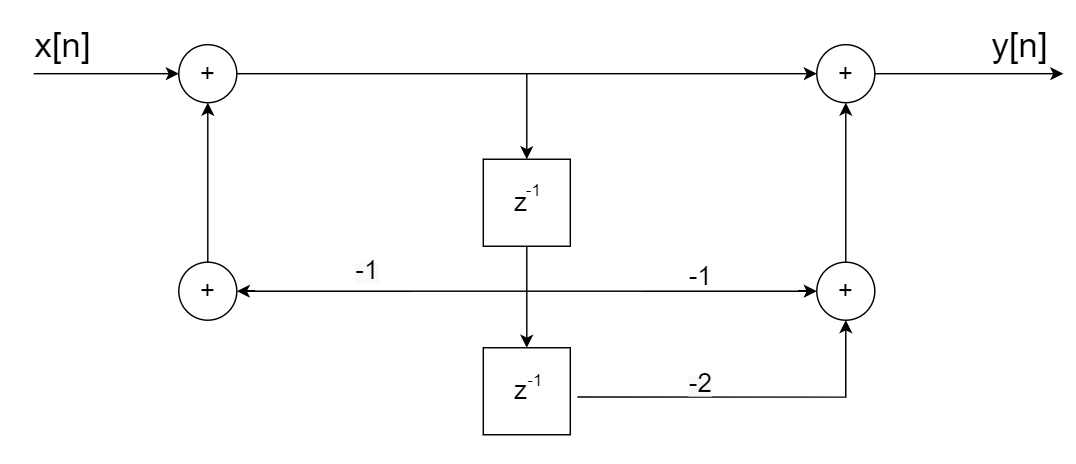
1. 求$ H(z) $
2. 求该系统的差分方程
3. 求当$ n=0,1,2,3,4 $时,$ h[n] $的值
4. 已知输入信号为:$ x[n]=\left{\begin{matrix} 1 & n=0 \ -1 & n=1 \ 0 & other \end{matrix}\right. $ 求$ y[n] $
七、